Linear Algebra

Linear algebra is one of the important branches of mathematics.
Linear algebra is basically the study of vectors and linear functions.
It is a key concept for almost all areas of mathematics.
Linear algebra is considered a basic concept in the modern presentation of geometry.
It is mostly used in Physics and Engineering as it helps to define the basic objects such as planes,
lines, and rotations of the object. It allows us to model many natural phenomena, and also it has computing efficiency.
In this article, you are going to learn about the basic introduction,
its components, problems, linear equations, and its applications.
Introduction to Linear Algebra
Linear algebra is the study of linear combinations. It is the study of vector spaces, lines, planes, and some mappings that are required to perform linear transformations. It includes vectors, matrices, and linear functions. It is the study of linear sets of equations and their transformation properties.
The general linear equation is represented as:
a1x1 + a2x2 + ... + anxn = b
Here:
a - represents the coefficients
x - represents the unknowns
b - represents the constant

There exists a system of linear algebraic equations, which is a set of
equations. The system of equations can be solved using matrices.
It obeys the linear function such as:
(x1, ..., xn) → a1x1 + ... + anxn

Vector Spaces
As we know that linear algebra deals with the study of vector spaces and
the linear transformations between them. By the definition of a vector, it is a
physical quantity that has both magnitude and direction. A vector space is
defined as the collection of objects called vectors, which may be added
together and multiplied (i.e. scaled) by numbers, called scalars. Generally,
real numbers are taken as scalars, but there exist vector spaces with scalar
multiplication by non-real numbers, i.e., complex numbers, or naturally any
field.
The operations such as vector addition and scalar multiplication must
satisfy specific requirements, called vector axioms. Generally, the terms
real vector space and complex vector space are used to define that the
scalars are real or complex numbers, respectively.
Suppose V be any vector space with elements a, b, c and scalars m, n over
a field F, then the vector axioms are given by:
Commutative of addition: a + b = b + a
Associativity of addition: a + (b + c) = (a + b) + c
Additive identity: a + 0 = 0 + a = a, where 0 is an element in V called
the zero vector.
Additive inverse: a + (-a) = 0, where a and -a belong to V.

Other axioms include distributivity of scalar multiplication with respect to
vector addition and field addition, identity element of scalar multiplication,
and so on.
For example: m(a) = ma; n(a + b) = na + nb
An element of a specific vector space may have different characteristics.
For example, the elements can be a sequence, a function, a polynomial, or a
matrix. Linear algebra is affected by the properties of such elements that are
common or familiar to all vector spaces.
A linear map can be written for two given vector spaces, namely V and W,
over a field F. This is sometimes referred to as a linear transformation or
mapping of vector spaces. Thus, it is given by:
T: V → W
This allows us to write the addition and scalar multiplication of elements
such as:
T(a + b) = T(a) + T(b)
T(ma) = mT(a)
Linear Function
A linear function is an algebraic equation in which each term is either a
constant or the product of a constant and a single independent variable of
power 1. In linear algebra, vectors are used when forming linear functions.
Some examples of vectors can be rephrased in terms of the function of vectors.
Mathematically, a linear function is defined as:
A function L : Rn → Rm is linear if:
(i) L(x + y) = L(x) + L(y)
(ii) L(αx) = αL(x)
for all x, y ∈ Rn, α ∈ R.
Linear Algebra Matrix
Matrices are linear functions of a certain kind. A matrix is the result of
organizing information related to certain linear functions. Matrices frequently
appear in linear algebra because they are central to understanding its core
concepts.
Mathematically, this relation can be defined as follows:
A is an m × n matrix, then we get a linear function L : Rn → Rm by defining:
L(x) = Ax
or
Ax = B
Go through the example below to understand this mapping in detail.
Question:
A room contains x bags and y boxes of fruits. Each bag contains 2 apples
and 4 bananas, and each box contains 6 apples and 8 bananas. There are a
total of 20 apples and 28 bananas in the room. Find the value of x and y.
Solution:
Write the simultaneous equations for the given information that satisfies the
conditions:
2x + 6y = 20
4x + 8y = 28

Numeric Linear Algebra
Numerical linear algebra is also known as the applied linear algebra. Applied linear algebra deals with the study of how matrix operations can be used to create computer algorithms, which helps to solve the problems in continuous mathematics with efficiency and accuracy. In numerical linear algebra, many matrix decomposition methods are used to find the solutions for common linear algebraic problems like least-square optimization, locating Eigenvalues, and solving systems of linear equations. Some of the matrix decomposition methods in numerical linear algebra include Eigen decomposition, Single value decomposition, QR factorization and so on.
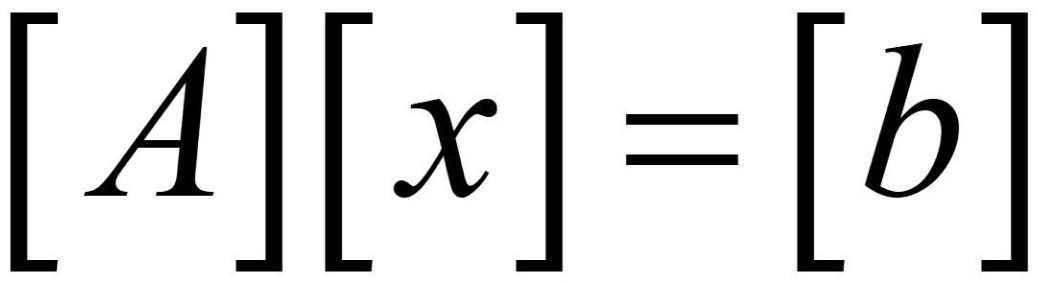
Linear Algebra Applications
Here, some of the linear algebra applications are given as:
- Ranking in Search Engines: One of the most important applications of linear algebra is in the creation of Google. The most complicated ranking algorithm is created with the help of linear algebra.
- Signal Analysis: It is massively used in encoding, analyzing, and manipulating signals that can be either audio, video, or images, etc.
- Linear Programming: Optimization is an important application of linear algebra, which is widely used in the field of linear programming.
- Error-Correcting Codes: It is used in coding theory. If encoded data is tampered with slightly, linear algebra can help recover it. One such important error-correcting code is called Hamming code.
- Prediction: Predictions of some objects can be made using linear models, which are developed using linear algebra.
- Facial Recognition: An automated facial recognition technology that uses linear algebraic expressions is called principal component analysis.
- Graphics: An important part of graphics is projecting a 3-dimensional scene onto a 2-dimensional screen, which is handled only by linear maps explained by linear algebra.