Isosceles Triangle

An isosceles triangle is a type of triangle that has any two sides equal
in length. The two angles of an isosceles triangle, opposite to equal
sides, are equal in measure. In geometry, triangle is a three-sided polygon
that is classified into three categories based on its sides, such as:
- + Scalene triangle (All three sides are unequal)
- + Isosceles triangle (Only two sides are equal)
- + Equilateral triangle (All three sides are equal)
In this article, we will learn the properties and formulas related to the isosceles triangle, in detail, along with examples.
Fun Fact:
Did you know that the isosceles triangle played a starring role in ancient architecture?
The Great Pyramid of Giza, one of the Seven Wonders of the Ancient World, incorporates isosceles triangles in its design.
Each triangular face of the pyramid is an isosceles triangle, symbolizing strength and stability—a perfect
blend of beauty and engineering that has stood the test of time!
What is Isosceles Triangle?
An Isosceles triangle is a triangle that has two equal sides. Also, the two angles opposite the two equal sides are equal. In other words, we can say that “An isosceles triangle is a triangle which has two congruent sides“. Suppose in a triangle △ABC, if sides AB and AC are equal, then △ ABC is an isosceles triangle where ∠ B = ∠ C. The theorem that describes the isosceles triangle is “if the two sides of a triangle are congruent, then the angle opposite to them are also congruent”.
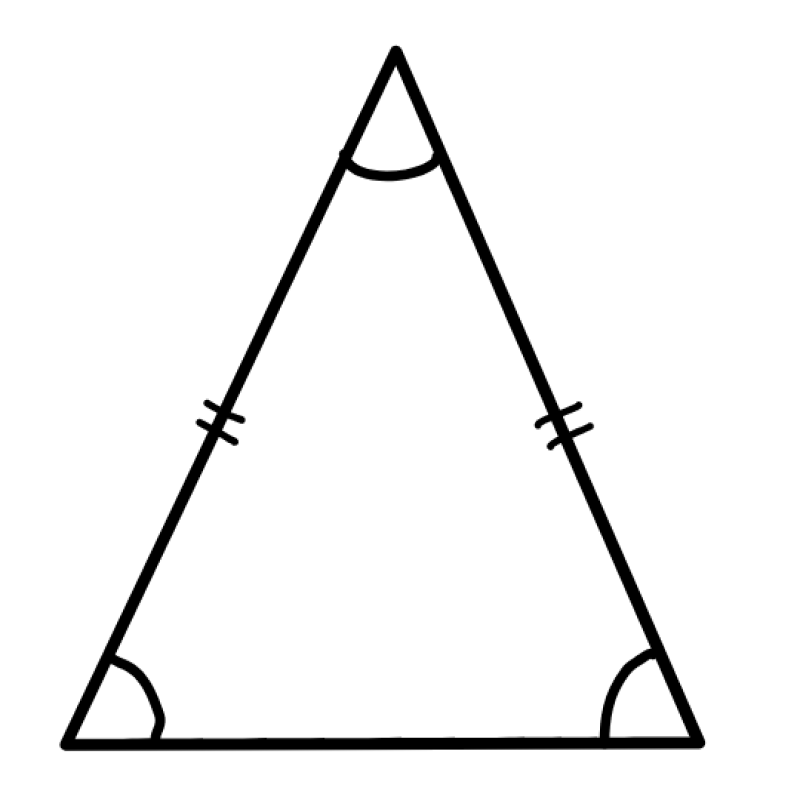
Angles of Isosceles Triangle
The two of the three angles of the isosceles triangle are equal in measure, which is opposite to the equal sides. Hence, one of the angles is unequal. Suppose, if the measure of an unequal angle is given to us, then we can easily find the other two angles by angle sum property.
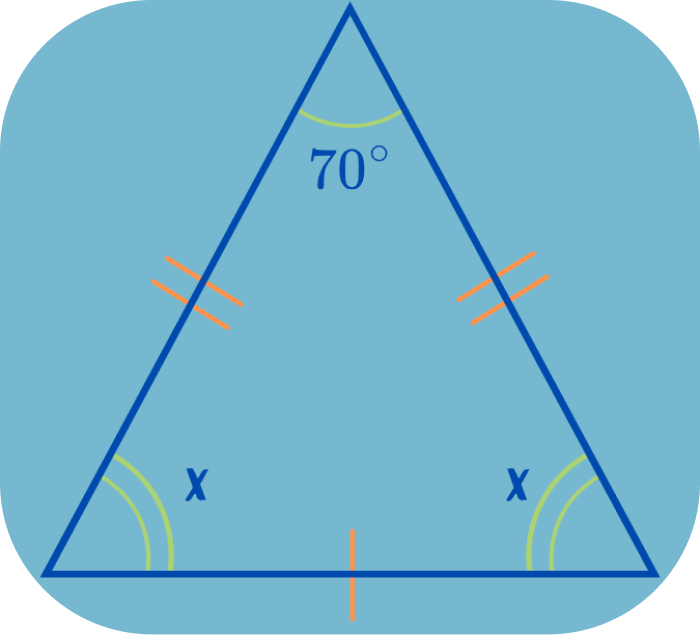
Example: Given an isosceles triangle.
Let the measure of the unequal angle is 70° and the other two equal angles measures x; then, as per the angle sum rule,
70° + x + x = 180°
70° + 2x = 180°
2x = 180 – 70 = 110°
x = 110/2 = 55°
Hence, the measure of the other two angles of an isosceles triangle is 55°.
Properties of Isosceles Triangle
- As the two sides are equal in this triangle, the unequal side is called the base of the triangle.
- The angles opposite to the two equal sides of the triangle are always equal.
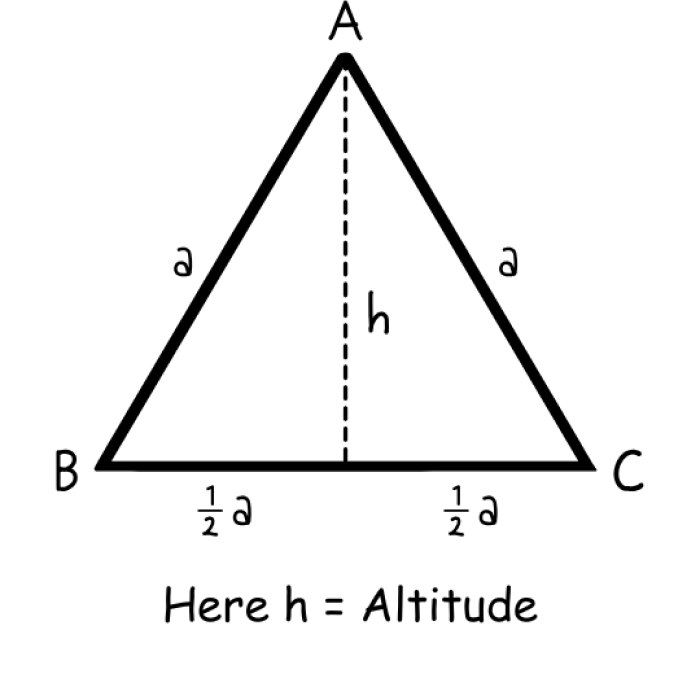
- The altitude of an isosceles triangle is measured from the base to the vertex (topmost) of the triangle.
- A right isosceles triangle has a third angle of 90 degrees.
Isosceles Triangle Theorem
As per the theorem, if two sides are congruent in an isosceles triangle, then the angles opposite to the two sides are also congruent.
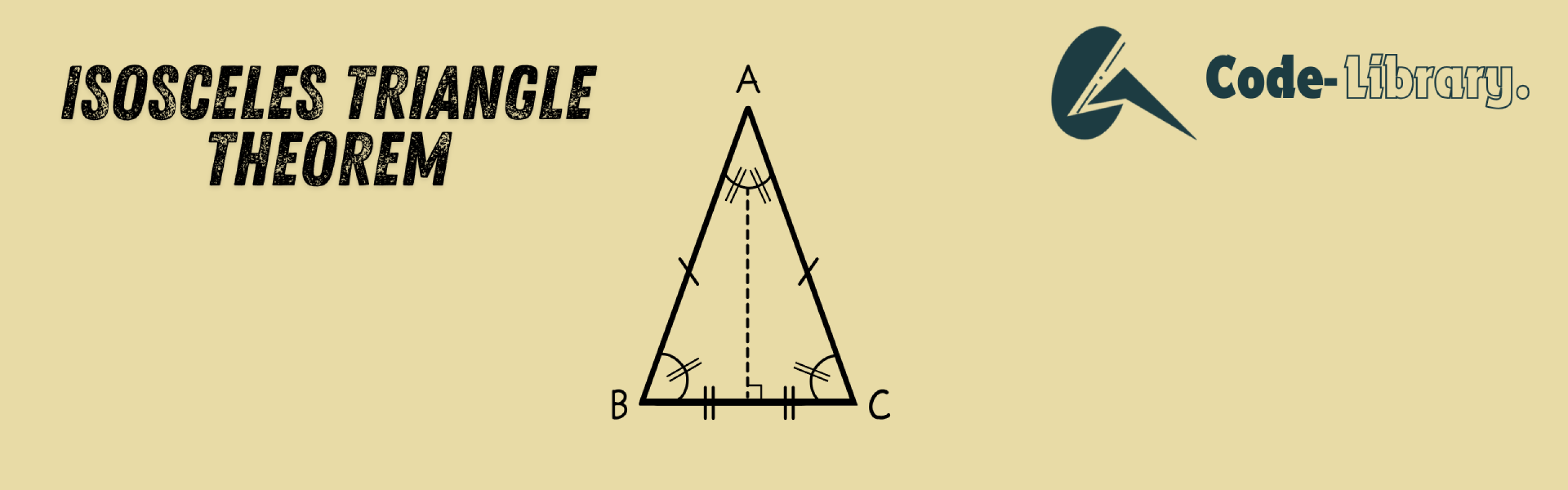
Alternatively, if two angles are congruent in an isosceles triangle, then the sides opposite to them are also congruent.
In the above triangle ABC,
AB = AC
∠ABC = ∠ADC
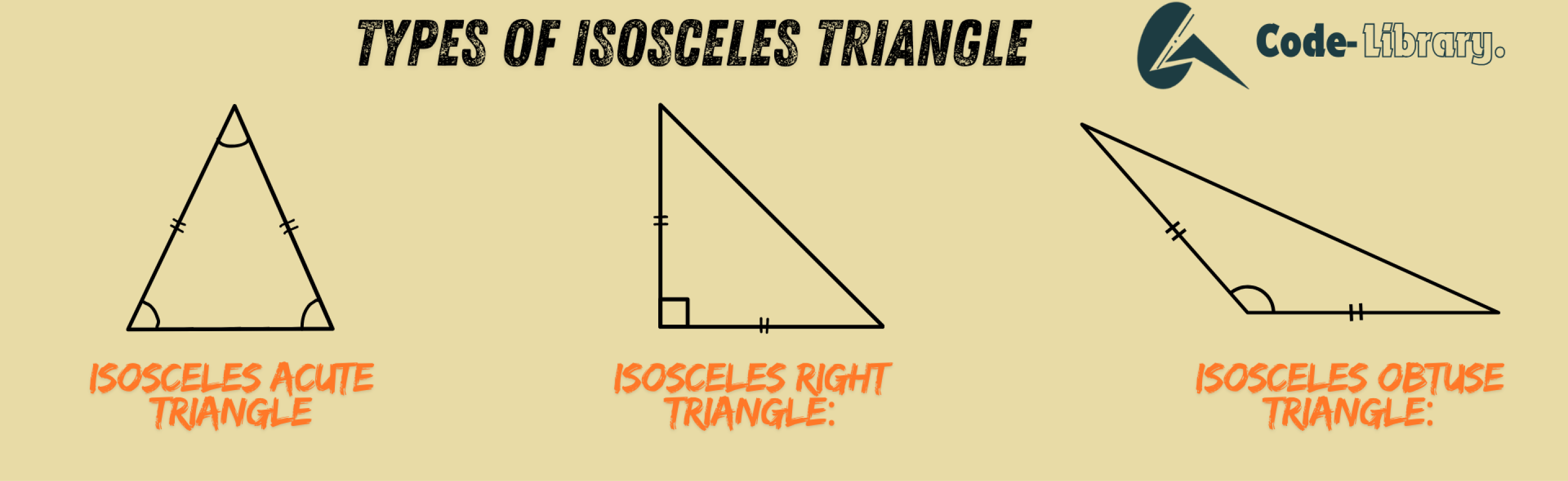
Types of Isosceles Triangle
Generally, the isosceles triangle is classified into different types, namely,
- - Isosceles acute triangle
- - Isosceles right triangle
- - Isosceles obtuse triangle
Now, let us discuss these three different types of an isosceles triangle in detail.
Isosceles acute triangle
As we know that the different dimensions of a triangle are legs, base, and height. All the isosceles triangle has an axis of symmetry along the perpendicular bisector of its base. Depending on the angle between the two legs, the isosceles triangle is classified as acute, right and obtuse. The isosceles triangle can be acute if the two angles opposite the legs are equal and are less than 90 degrees (acute angle).
Isosceles right triangle
A right isosceles triangle has two equal sides, wherein one of the two equal sides acts as perpendicular and another one as a base of the triangle. The third side, which is unequal, is termed the hypotenuse. Therefore, we can apply here the famous Pythagoras theorem, where the square of the hypotenuse is equal to the sum of the square of base and perpendicular.
Suppose the sides of the right isosceles triangle are a, a, and h, where a is the two equal sides, and h is the hypotenuse, then;
h = √(a2 + a2) = √2a2 = a√2 or h = √2a
Isosceles obtuse triangle
We know that the obtuse triangle is a triangle in which one of its angles is greater than 90 degrees (right angle). Also, drawing a triangle with more than two obtuse angles is impossible. We know that the obtuse triangle can be a scalene triangle or isosceles triangle. Therefore, the isosceles obtuse triangle is a triangle which has two equal sides with an obtuse angle.
Isosceles Triangle Formulas
We know that an isosceles triangle is a two-dimensional shape with three sides. The measures to compute the isosceles triangle are the area and perimeter. Now, let us discuss the area and the perimeter of the isosceles triangle in detail.
Area of Isosceles Triangle:
The area of an isosceles triangle is defined as the region occupied by it in the two-dimensional space. Generally, the isosceles triangle is half the product of the base and height of an isosceles triangle. The formula to calculate the area of an isosceles triangle is given by:
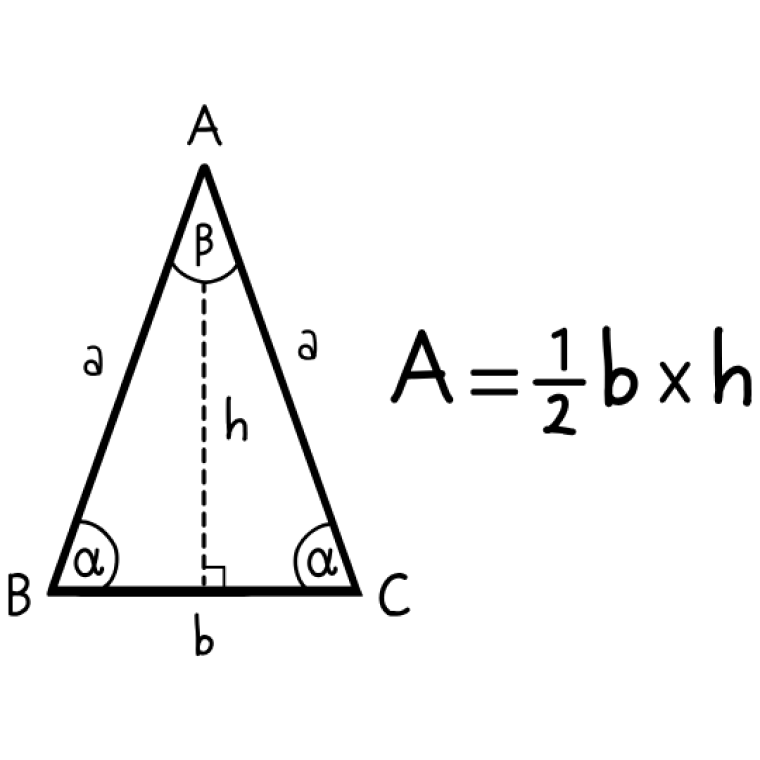
The area of an isosceles triangle, A = 1/2 x b x h square units
where b is the base and h is the triangle's height.
Perimeter of Isosceles Triangle:
As we know, the perimeter of any shape is the shape’s boundary. Similarly, the perimeter of an isosceles triangle is defined as the sum of the three sides of an isosceles triangle. The perimeter of an isosceles triangle can be found if we know its base and side. The formula to calculate the perimeter of the isosceles triangle is given by:
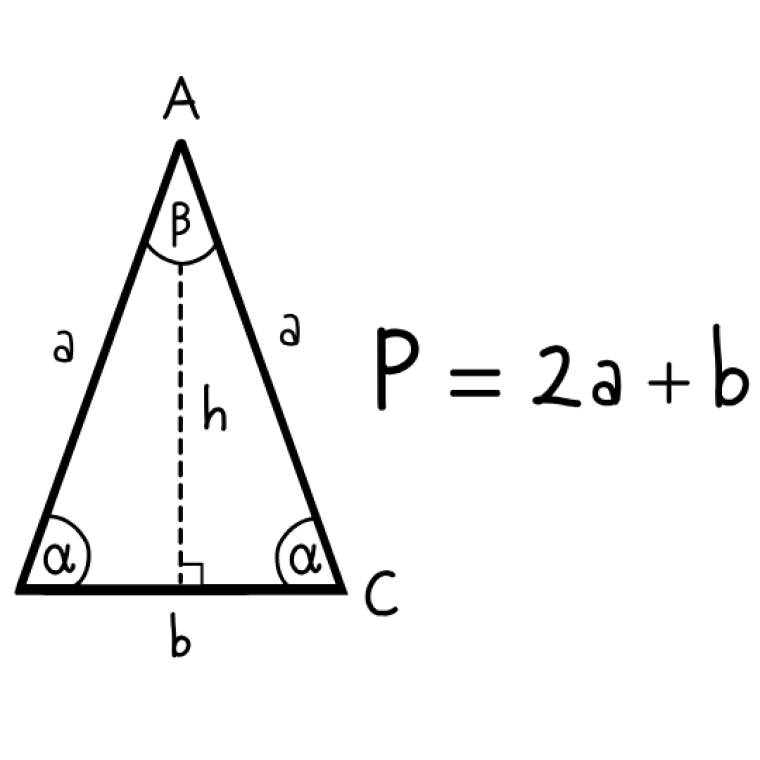
The perimeter of an isosceles triangle, P = 2a + b units
where a is the lenght of the two equal legs of the triangle and b is the base of the triangle.
Altitude of Isosceles Triangle:
When an altitude is drawn to the base of the isosceles triangle, it bisects the vertex angle. As it bisects the base, the two congruent triangles are created. The altitude of the triangle forms the required right angle and the altitude becomes the shared legs. Also, the congruent legs of a triangle become the congruent hypotenuse. Therefore, the altitude of drawn to the base of the isosceles triangle bisects the base.