Shopping Cart

Shopping Cart

Corresponding Angles

Definition: Corresponding angles are the angles which are formed in matching corners or corresponding corners with the transversal when two parallel lines are intersected by any other line (i.e. the transversal). For example, in the below-given figure, angle p and angle w are the corresponding angles.

corresponding_angles
Corresponding Angles Examples and Types

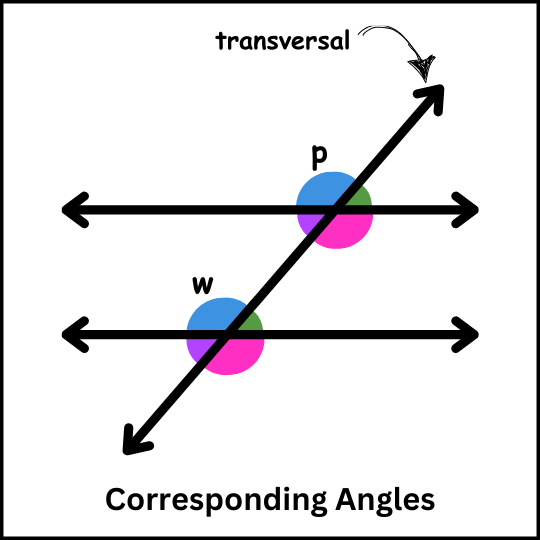
Examples of the corresponding angle are any angles which are formed on the opposite side of the transversal. Now, it should be noted that the transversal can intersect either two parallel lines or two non-parallel lines. Thus, corresponding angles can be of two types:

Here we will discuss only corresponding angles formed by the intersection of two lines by a transversal. The two lines could be parallel or non-parallel. So, let us learn corresponding angles for both the cases.

Corresponding Angles Formed by Parallel Lines and Transversals:

If a line or a transversal crosses any two given parallel lines, then the corresponding angles formed have equal measure. In the given figure, you can see, the two parallel lines are intersected by a transversal, which forms eight angles with the transversal. So, the angles formed by the first line with the transversal have equal corresponding angles formed by the second line with the transversal.

Angles formed by parallel lines and transversal

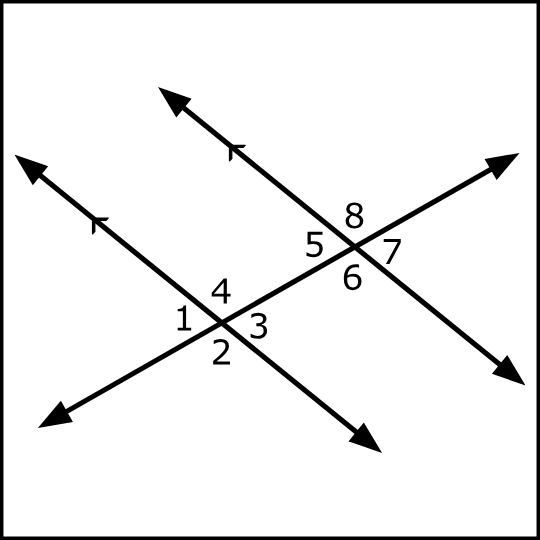
All corresponding angle pairs in the figure:

Note:

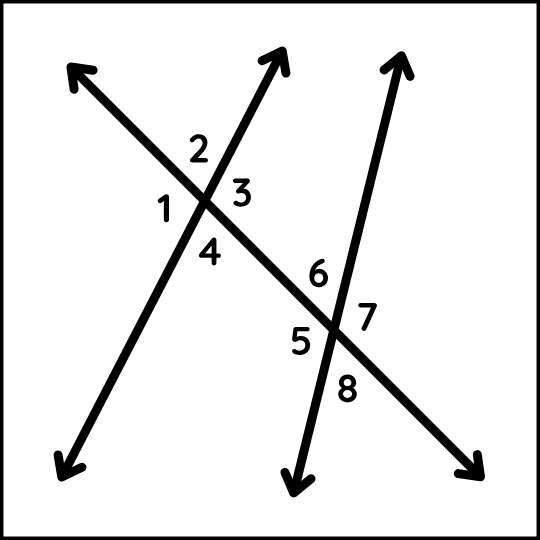
Corresponding Angles Formed by Non-Parallel Lines and Transversals:

For non-parallel lines, if a transversal intersects them, then the corresponding angles formed doesn’t have any relation with each other. They are not equal as in the case of parallel lines but all are corresponding to each other.

Angles formed by non-parallel lines and transversal
Corresponding Angles Theorem

According to the corresponding angles theorem, the statement “If a line intersects two parallel lines, then the corresponding angles are congruent (equal)” is true either way. This theorem is also termed as "corresponding angles postulate".

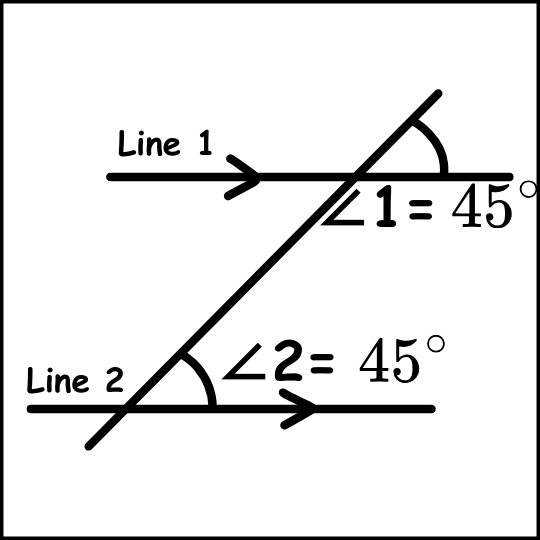
Diagram showing corresponding angles theorem
The Converse of Corresponding Angles Theorem

The corresponding angles converse theorem would be, “If the corresponding angles are congruent, then the two lines are said to be parallel.”

What if a transversal intersects two lines and the pair of corresponding angles are equal? Then, the two lines intersected by the transversal are said to be parallel. This is the converse of the corresponding angle theorem.

Important Notes on Corresponding Angles:


Square Root

Terms and Conditions

REFUND POLICY:

1. Eligibility for Refunds:
- Parents can request a refund only after commencing the regular classes and within 60 days from the date of enrollment.
- Refund requests made after 60 days from the date of enrollment will not be considered.

2. Unused Classes:
- Unused classes can be converted into credits which can be redeemed later across any course at Code Library.
- These credits must be used within Two year from the date of issuance, after which they will expire.

3. Cash Refunds:
- Parents are eligible for a pro-rated refund corresponding to the number of unused classes.
- A service fee of $99 will be deducted from the refund amount if a cash refund is requested.

4. Installment/Subscription Plans:
- Parents paying in installments or subscription plans are eligible for a pro-rated refund only in the case of an identified service lapse from Code Library's end.
- The service lapse must be reported within 72 hours of its occurrence through our official support email or WhatsApp channel.
- If the service lapse is not resolved within 72 hours of reporting, the pro-rated refund will be processed.

5. Service Lapses:
- Service lapses include technical issues, instructor unavailability, or any other issue that prevents the scheduled class from taking place.
- The decision on what constitutes a service lapse is at the sole discretion of Code Library.

6. Refund Processing:
- Refunds will be processed within 14 business days from the date of approval.
- Refunds will be credited back to the original mode of payment used during enrollment.


CANCELLATION POLICY:

1. Class Cancellations by Students:
- Students can cancel or reschedule a maximum of 6 sessions per 48 sessions.
- Cancellations or rescheduling must be done at least 24 hours prior to the scheduled class time.
- Failure to cancel or reschedule within this timeframe will result in the session being marked as a "No Show."

2. No Show Policy:
- If a student does not join a class without prior cancellation, it will be treated as a "Student No Show."
- "No Show" sessions will be marked as completed and will not be eligible for rescheduling or compensation.

3. Instructor Cancellations:
- In the event of a class cancellation by the instructor, the session will be rescheduled at a mutually convenient time without any penalty to the student.
- If rescheduling is not possible, the session will be converted into credits which can be used for future classes.

4. Extenuating Circumstances:
- In case of medical emergencies or other extenuating circumstances, students can appeal for exceptions to the cancellation policy.
- Such appeals must be supported by relevant documentation and will be considered on a case-by-case basis.


PRIVACY POLICY:

1. Information Collection:
- We collect personal information including but not limited to names, contact details, payment information, and usage data to provide and improve our services.


2. Use of Information:
- Personal information is used to facilitate course enrollment, provide customer support, process payments, and communicate with users.
- We may use anonymized data for analytical purposes to enhance our services.

3. Information Sharing:
- We do not share personal information with third parties except as necessary to provide our services or comply with legal obligations.
- Third parties involved in service delivery (e.g., payment processors) are obligated to maintain the confidentiality of the information.

4. Data Security:
- We implement appropriate technical and organizational measures to protect personal information against unauthorized access, disclosure, alteration, or destruction.

5. User Rights:
- Users have the right to access, correct, or delete their personal information held by us.
- Requests can be made via our support email and will be addressed within a reasonable timeframe.

6. Policy Updates:
- Our privacy policy may be updated from time to time. Users will be notified of any significant changes via email or through our website.





Sincerely,
Code Library Team